CREATING A CLASSIFIER

OBJECTIVE

design a function that takes image as input and responds with a label

A POSSIBLE TECHNIQUE, IMAGE FLATTENING

The idea is to scan linearly the image pixels:

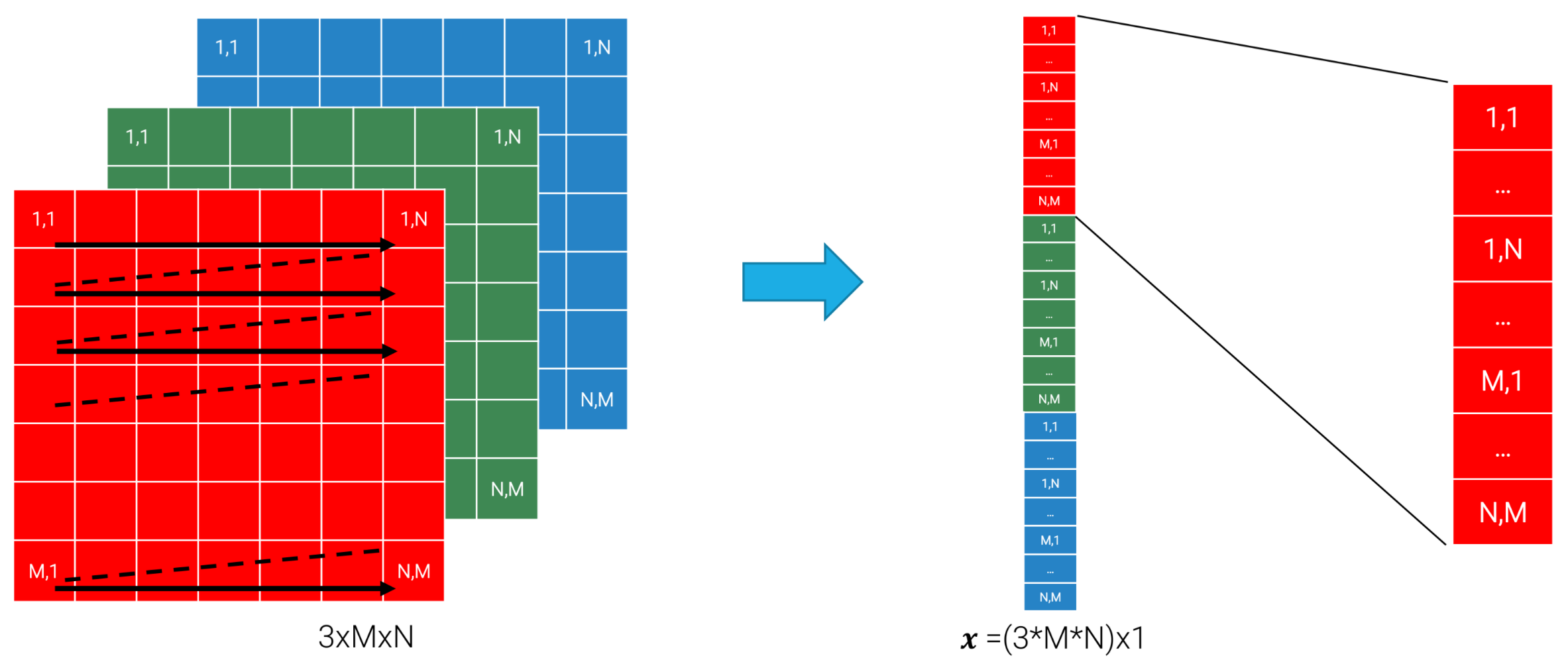
so the classifier becomes:

$$f(x,W)=Wx=label$$

where $W$ is a linear vector of $3\times M\times N$ size as the $x$ input.

LIMITS OF IMAGE FLATTENING

This solution is not practical cause the label is a categorical and not numerical value so closer values do not imply that images are of similar classes

A better choice is to output scores for each label so

$$f(x,W)=Wx=scores$$

where $W$ is a matrix of size $(3\times M\times N)\times nlabels$ and scores is a vector of size $nlabels$

This type of linear classifier can be realize with the template matching approach Where templates are rows of the $W$ matrix

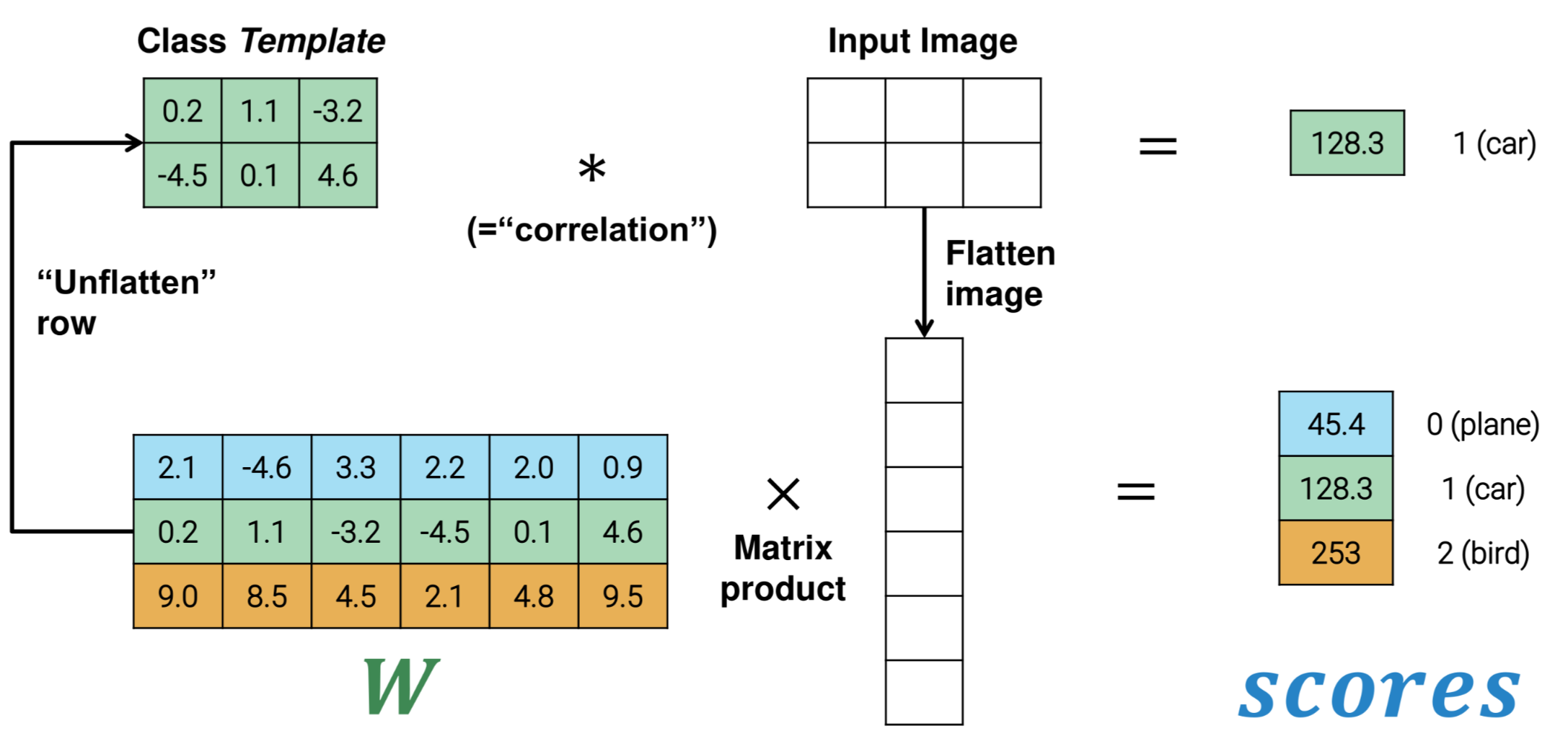
LOSS FUNCTION FOR A LINEAR CLASSIFIER

A common approach is to translate the scores in probabilities with the softmax function

$$softma{x}_j(s)=\frac{exp(s_j)}{{\sum }_{k=1}^{C}exp(s_k)}$$

the true label can be represented as a one hot encoded row of scores such as

$$\left[\begin{array}{ccccccccc}0& 0& 0& ...& 1& ...& 0& 0& \end{array}\right]$$

The loss function must be a function that decrease as the probability given by the model becomes higher

$$L(\theta ,(x^{(i)},y^{(y)}))=-\log p_{model}(y=y^{(i)}|x=x^{(i)};\theta )$$ $$L(\theta ,D^{train})=\sum _{i=1}^N-\log p_{model}(y=y^{(i)}|x=x^{(i)};\theta )$$

So in the case of a linear classifier the $-\log p_{model}(y=y^{(i)}|x=x^{(i)};\theta )$ function can be defined as

$$-\log p_{model}(y=y^{(i)}|x=x^{(i)};\theta )=\frac{exp(s_j)}{{\sum }_{k=1}^{C}exp(s_k)}$$

so the per sample loss is given by:

$$-\log \frac{exp(S_y(i))}{{\sum }_{k=1}^{C}exp(s_k)}=S_y(i)+\log \sum _{k=1}^{C}exp(s_k)\simeq$$ $$-S_y(i)+\underset{k}{\max }{S}_k$$

MINIMIZING THE LOSS FUNCTION

The loss function can be seen as a multivariate function with the variables being the parameters of the model $\theta$ so the problem becomes an optimization problem of the type

$$argmi{n}_{\theta \in \Theta }(L(\theta ,D^{train}))$$

The most common approach to this problem is to compute the gradient of the loss function

$$\nabla L(\theta ,D^{train})=\left[\begin{array}{c}\frac{\delta L(\theta ,D^{train})}{\delta {\theta }_1}\\ ⋮\\ \frac{\delta L(\theta ,D^{train})}{\delta {\theta }_k}\end{array}\right]$$

and follow his direction (GRADIENT DESCENT)

GRADIENT DESCENT

• Randomly initialize ${\theta }^{(0)}$

for $e=1,..,E$ epochs:

• Forward pass classify all training data to get the predictions and the loss function
• Backward pass compute the gradient $\nabla L$
• Update parameters ${\theta }^{(e)}={\theta }^{(e-1)}-\alpha \nabla L$ where $\alpha$ is the learning rate hyper parameter

The learning rate can influence the convergence speed of the training procedure:

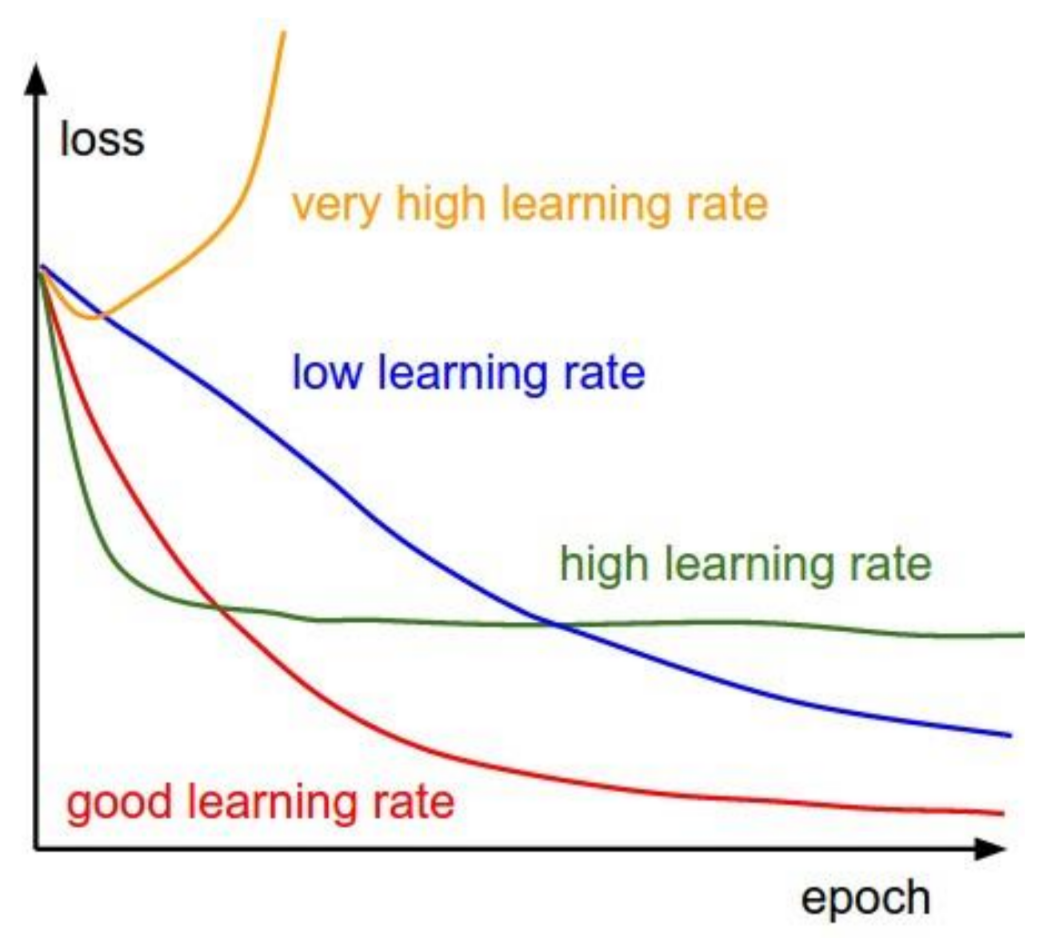
GRADIENT DESCENT LIMITS

Computing the gradient of the loss function on all the training data results in a computational infeasible task as the the loss function is the mean of the per-sample losses the gradient needs to be computed on ALL of the samples

STOCASTIC GRADIENT DESCENT

Instead of computing the gradient on the global loss function the parameter update is done for each sample, this method is more computationally efficient but is not robust to noise

BEST COMPROMISE

A good compromise can be to use mini data batches to compute the gradient choosing a batch of $B$ size ($B$ is also an hyperparameter), the number of updates in each epoch (e.g. the number of batches ) can be computed as $\frac{N}{B}$

In this case larger batches approximate better the gradient at the cost of memory occupation

IMPROVEMENT ON THE APPROXIMATIONS

In order to improve further the approximation a momentum parameter to the update phase can be deployed:

$$\beta \in [0,1),v^{(0)}=0$$ $$\{\begin{array}{l}{v}^{(t+1)}=\beta v^{(t)}-\alpha \nabla L({\theta }^{(0)})\\ {\theta }^{(t+1)}={\theta }^{(t)}+v^{(t+1)}\end{array}$$

With this parameter the update becomes a mean of the previous ones smoothing the gradient

LIMITS OF A LINEAR CLASSIFIER

For a lot of application capture all the variability with one template is impossible, there is the need of something more meaningful than row pixels. There is the need to transform pixels in some form of feature

PREVIOUS NEXT