IMAGE FILTERS

Image filters are operators that given a 2D input image calculate the new intensity of a pixel based on considerations on the neighborhood, an important class of filters are the linear and translation equivariant filters.

LTE filters are olso used in CNN as feature extractors

LINEAR AND TRANSLATION EQUIVARIANT FILTERS

LINEARITY

given a 2D input signal $i(x,y)$ an operator $T(i(x,y)):T(i(x,t))=o(x,y)$ is linear if the filter of a linear combination is equal to the output of the filters of the single elements

$$T(a{i}_1(x,y)+b{i}_2(x,y))=a{o}_1(x,y)+b{o}_2(x,y)with$$ $$o_1(.)=T(i_1(.)),o_2(.)=T(i_2(.))b,y\in R$$

TRANSLATION EQUIVARIANCY

an operator $T(i(x,y)):T(i(x,t)=o(x,y)$ is said to be translation equivariant if the output of the filter given an image with translated coordinates is the same as the output of the filter for that given points

$$T(i(x-x_0,y-y_0))=o(x-x_0,y-y_0)$$

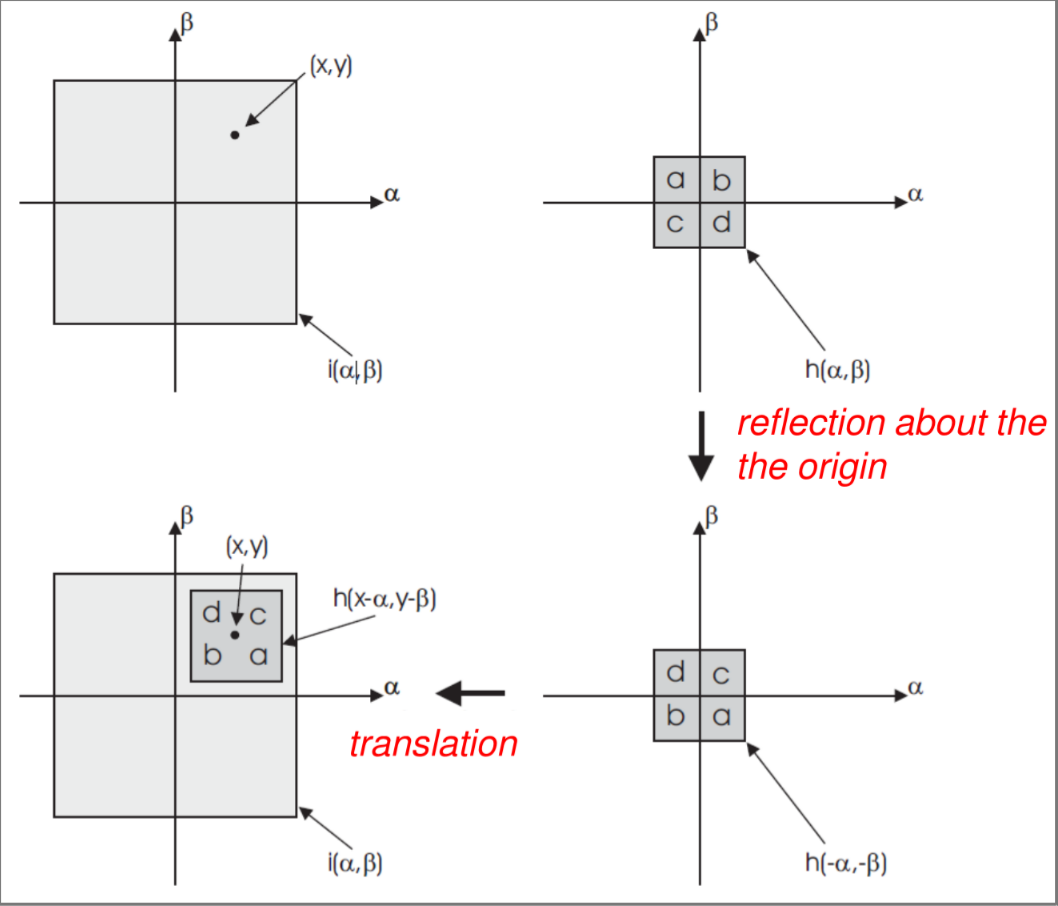
CONVOLUTION

If this conditions are met then the output of the operator is given by the convolution between the input signal and the impulse response (kernel) of the operator.

$$o(x,y)=T(i(x,y))={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }i(\alpha ,\beta )h(x-\alpha ,y-\beta )d\alpha d\beta with$$ $$h(x,y)=T(\delta (x,y))$$

PROPERTIES

The convolution $o(x,y)=i(x,y)\ast h(x,y)$ benefits from the following properties

PROPERTY	FORMULA
associative	$f\ast (g\ast h)=(f\ast g)\ast h$
commutative	$f\ast g=g\ast f$
distributive wrt to the sum	$f\ast (g+h)=f\ast g+f\ast h$
commutative wrt differentiation	$(f\ast g{)}^{{}^{\prime }}=f^{{}^{\prime }}\ast g=f\ast g^{{}^{\prime }}$

CORRELATION

correlation of a signal $i(x,y)$ with respect to a signal $h(x,y)$ is defined as follows

$$i(x,y)\circ h(x,y)={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }i(\alpha ,\beta )h(x+\alpha ,y+\beta )d\alpha d\beta with$$

CORRELATION IS NOT COMMUTATIVE

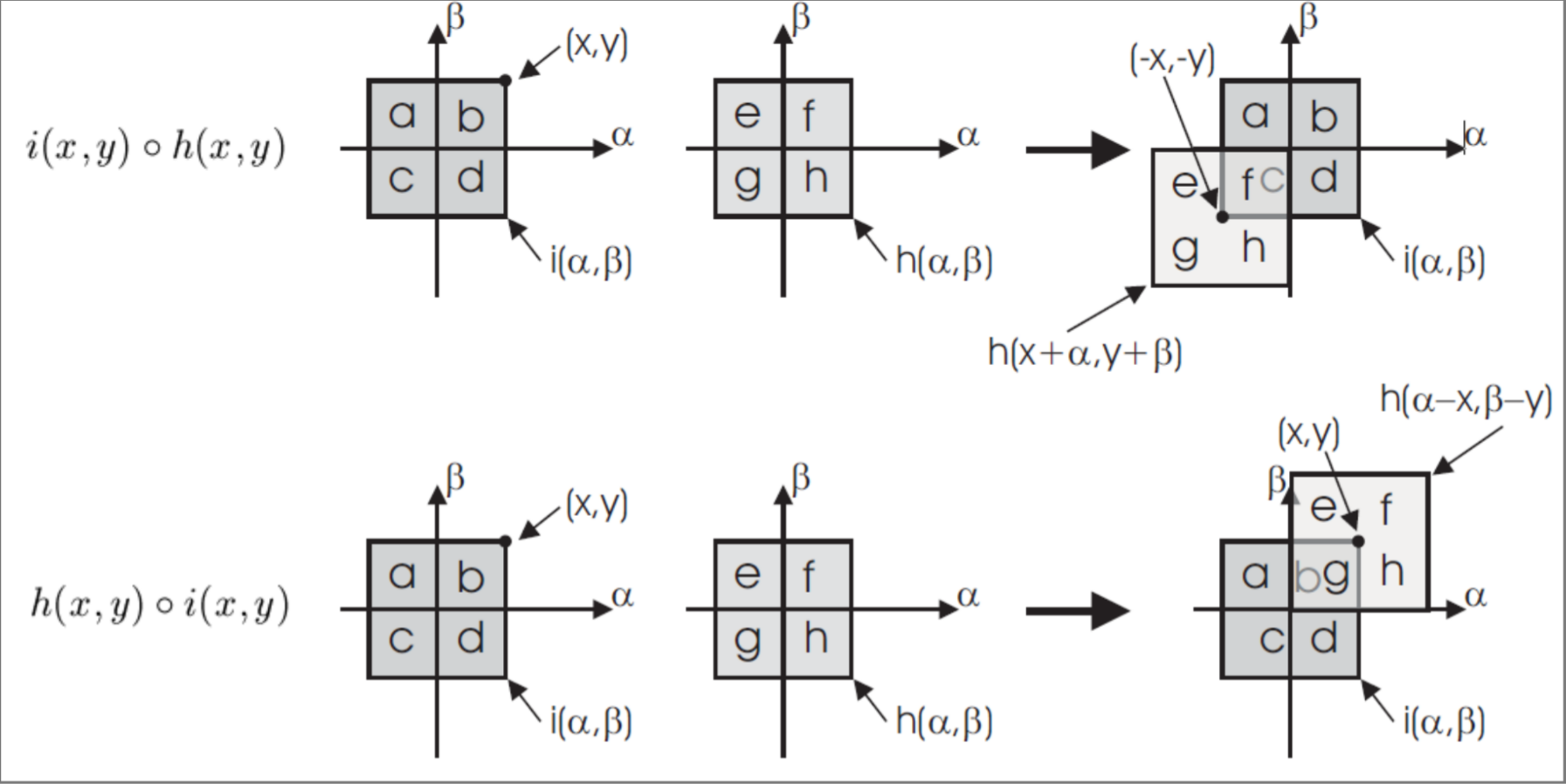
CONVOLUTION AND CORRELATION RELATION

Convolution and correlation are similar to each other, they both integrate a product of 2 functions after translation (but correlation does not do reflection), it’s worth to notice that if the $h(x,y)$ function is even the 2 functions are equal:

$$i(x,y)\ast h(x,y)=h(x,y)\ast i(x,y)={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }i(\alpha ,\beta )h(x-\alpha ,y-\beta )d\alpha d\beta =$$ $${\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }i(\alpha ,\beta )h(\alpha -x,\beta -y)d\alpha d\beta =$$ $$h(x,y)\circ i(x,y)$$

Remember that correlation is not commutative even if h is even

DISCRETE CONVOLUTION

In a real scenario the image is a discrete representation, in order to account for this the convolution function is translated in a discrete form

$$O(i,j)=T(I(i,j))=\sum _{m=-\infty }^{+\infty }\sum _{n=-\infty }^{+\infty }I(m,n)H(i-m,j-n)with$$ $$H(i,j)=T(\delta (i,j))$$

In this representation the input and the output function are real image signals representations and the $H(i,j)$ is the discrete representation of the kernel function (e.g. the kronecker delta function)

This model it’s not feasible for implementation as images are stored on matrix of finite sizes

$$O(i,j)=\sum _{m=-k}^{+k}\sum _{n=-k}^{+k}K(m,n)I(i-m,j-n)with$$

So the idea behind the implementation is to slide the kernel matrix over the image and compute the convolution for each point of the image

PREVIOUS NEXT