Top-$k$ queries

l’obbiettivo quando si parla di top-$k$ queries e quello di fornire i primi $k$ risultati che più si avvicinano alla richiesta della query

Gli utilizzi più frequenti di questa tecnologia si hanno dei DB scientifici, motori di ricerca e-commerce sistemi multimediali

Approccio naive

La soluzione più banale al problema consiste nell’avere una scoring function $S$ che restituisce un punteggio in funzione dei valori della tupla.

to_be_sorted =[]
for tuple in R:
	# compute S for each tuple
	to_be_sorted.append({tuple,S(tuple)})
 
# sort based on S value and return the first k values
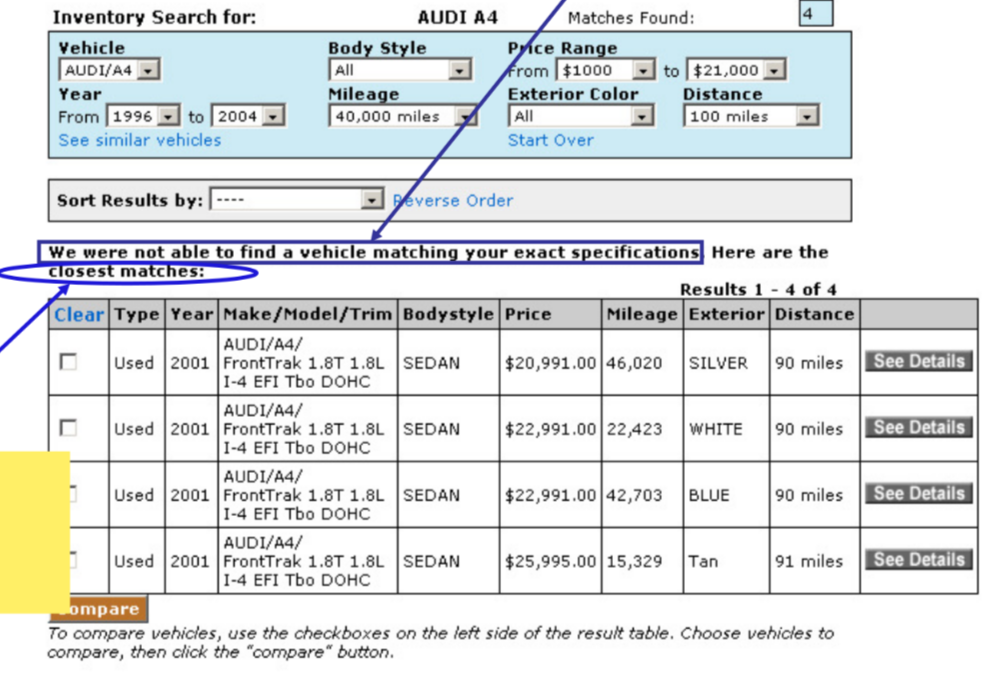
return to_be_sorted.sort().head(k)

questo approccio e estremamente costoso in quanto prevede il sorting di tutte le tuple, ancora peggio se la query prevede uno o più join

Inoltre si possono verificare casi di near miss o information overload, per esempio le query

SELECT * FROM  UsedCarsTable
WHERE Vehicle = ‘Audi/A4’ AND Price <= 21000
ORDER BY 0.8*Price + 0.2*Mileage
 
SELECT * FROM UsedCarsTable
WHERE Vehicle = ‘Audi/A4’
ORDER BY 0.8*Price + 0.2*Mileage

soffrono rispettivamente di escludere elementi con prezzo di poco maggiore ma un numero di chilometri estremamente basso (near-miss) e l’altra di dare in output tutti i veicoli di un dato modello (information overload)

Valutazione di una query top-$k$

Per la valutazione e necessario considerare due aspetti principali:

• numero di relazioni da accedere, valori aggregati
• modalità di accesso ai dati (indici in qualche attributo di ranking)

prendendo come riferimento la forma più semplice di query top-$k$

SELECT <some attributes>
FROM R
WHERE <Boolean conditions>
ORDER BY S(<some attributes>) 
STOP AFTER k

E necessario estendere l’algebra relazionale con un operatore ${\tau }_{k,S}$ che restituisca le $k$ tuple migliori secondo la funzione di scoring $S$

flowchart TD
top_operator --> filter --> Relation_R

Implementazione dell’operatore Top ${\tau }_{k,S}$

L’operatore top può essere implementato in due modalità

• top-scan la stream di tuple in ingresso e già ordinata e di conseguenza e sufficiente fornire in output le prime $k$ tuple

questo operatore puo lavorare in pipeline

• top-sort la stream non e ordinata e l’operatore la deve ordinare per poi fornire le tuple in output

questa implementazione non può lavorare in pipeline in quanto necessita di fare sorting

top-sort operator

Per implementare l’operatore top-sort e sufficiente allocare un buffer $B$ che contenga le $k$ tuple, ad ogni tupla letta la si confronta con la $k$-esima già nel buffer e la si scarta se non maggiore

se una tupla non e maggiore dell'ultima migliore $k$-esima si presume non fara parte del risultato finale

Query top-$k$ multidimensionali

Le query top-$k$ coinvolgono spesso più di un attributo nella funzione di scoring $S$

SELECT *
FROM USEDCARS
WHERE Vehicle = 'Audi/A4'
ORDER BY 0.8*Price + 0.2*Mileage
STOP AFTER 5;

In questo caso la situazione e più complessa:

• se non si ha nessun indice non c’e’ altra soluzione che applicare l’operatore di top-sort

• Se si può sfruttare un indice sull’attributo di selezione (clausola WHERE) allora la situazione migliora ma dipende dalla selettività della selezione

senza selezione si sta nella merda....

Cosa possiamo fare se avessimo un indice sugli attributi di ranking?, come dovrebbe essere l’indice?

analizziamo la geometria :)

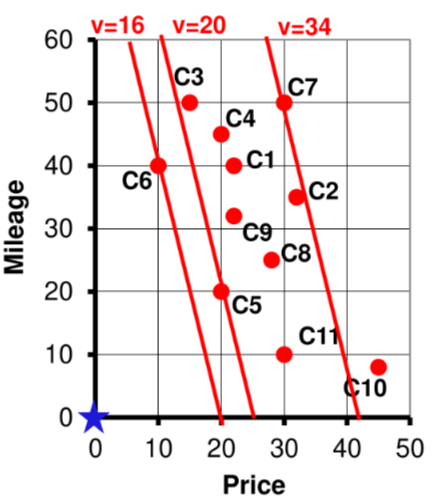
Se si plottano le tuple in un grafo basato sugli attributi di scoring si ottiene che le tuple che soddisfano la top-$k$ query si trovano tutte sotto una data linea

si considera di cercare macchine con i parametri di scoring più bassi possibili

Si può generalizzare a un punto qualunque dello spazio $q$, in questo caso si ottiene che i punti che soddisfano la top-$k$ query sono quelli all’interno di una regione di spazio intorno al punto di query $q$

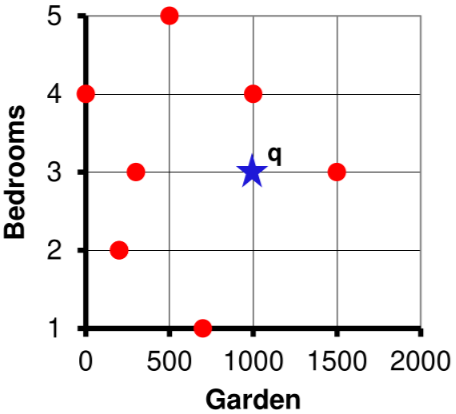
Di conseguenza il problema delle top-$k$ query si riduce al problema di trovare i $k$ nearest neighbors rispetto al query point $q$

top-$k$ query come problemi di $k$-NN

Di conseguenza il problema può essere modellato come segue, dato il seguente modello

• uno spazio $D$-dimensionale formato dagli attributi di scoring $A=(A_1,A_2,...,A_D)$
• una relazione $R(A_1,A_2,...,R_1,R_2,....)$
• un query point $q=(q_1,q_2,..,q_D)$
• una funzione $d:A\times A\to \Re$ che misura la distanza fra due punti di $A$

Il problema diventa:

dati un punto $q$ una relazione $R$, un intero $k\ge 1$ e una funzione distanza $d$ determinare le $k$ tuple in $R$ che sono le più vicine a $q$ secondo $d$

Risolvere query top-$k$ con indici

Una possibilità per risolvere le query top-$k$ e quello di usare b+tree multiattributo, questa soluzione non e ottimale. e molto meglio usare indici multidimensionali come i r-tree

i b+tree multi-attributo mostrano gli stessi problemi che si hanno in caso di window query

Determinare se un nodo contiene foglie utili: $d_{MIN}$ limite

Per determinare se un nodo dell’albero deve essere considerato in fase di ricerca si definisce la distanza del nodo come la distanza della foglia più vicina al punto di ricerca $q$

$$d_{MIN}(q,Reg(N))=inf\{d(q,p)|P\in Reg(N)\}$$

Di conseguenza si ha che se il nodo $N$ contiene punti interessanti deve essere vero che $d_{MIN}$ deve essere inferiore del raggio di ricerca $r$

$$Reg(q)\cap Reg(N)\ne \varnothing \iff d_{MIN}(q,Reg(N))\le r$$

Risolvere le query top-$k$: algoritmo KNNOptimal

Per risolvere le query con il modello sopracitato si introduce l’algoritmo KNNOptimal, l’algoritmo scandisce l’albero considerando i nodi $d_{MIN}(q,Reg(N))<r$ e memorizza la tupla $t$ con $d(q,t)$ minore

# query point input
q = {} 
 
# Initialize PQ with [ptr(RN),0];
PQ = []
PQ.append({ptr(RN),0})
rNN = 10000000;
while PQ.len() != 0:
	N = get_distance_and_point(PQ.pop())
	# read page from disk
	Read(N)
	if N is leaf:
		for t in N:
			if d(q,t) < rNN:
			
				# save tuple for result
				result = t
				# update search radius
				rNN = d(q,t)
				# update queue
				update(PQ)
	else:
		for Nc in N:
			if dMIN(q,Reg(Nc)) < rNN:
				ENQUEUE(PQ,[ptr(Nc), dMIN(q,Reg(Nc))])
return result, rNN

L’algoritmo KNNOptimal e corretto e I/O-ottimale in quanto accede solo pagine in cui e possibile trovare foglie vicine al risultato

KNNOptimal e query top-$k$ con filtro

In caso di query della forma

SELECT *
FROM USEDCARS
WHERE Vehicle = 'Audi/A4'
ORDER BY 0.8*Price + 0.2*Mileage
STOP AFTER 5;

non e detto che l’algoritmo KNNOptimal restituisca tuple concordi con il parametro di filtering, per supportare la casistica si utilizza una variante del KNNOptimal con supporto al distance browsing

nella coda PQ si includono anche le tuple e l’algoritmo termina quando il primo elemento della coda e una tupla

PREVIOUS NEXT