Top-$k$ join queries

Fino ad ora si sono prese in considerazione query top-$k$ con una sola relazione $R$, tuttavia e necessario considerare anche query della forma come segue:

SELECT <some attributes>
FROM R1,R2,…,Rn
WHERE <join and local conditions>
ORDER BY S(p1,p2,…pm)
STOP AFTER k

In realtà queste sono una generalizzazione del caso a singola relazione in cui la Relazione $R$ e spezzata in relazioni virtuali divise

SELECT *
FROM USEDCARS UC1, USEDCARS UC2, USEDCARS UC3
WHERE UC1.CarID = UC2.CarID
AND UC2.CarID = UC3.CarID
ORDER BY (UC1.Price + UC2.Mileage)/(UC3.Year-1970)
STOP AFTER 2

in questo caso i join sono tutti 1-1

Caso di studio per le top-$k$ 1-1 join queries

Il caso di studio che ha portato alla realizzazione delle prima soluzione per questa casistica e stato quello in cui le partizioni di $R$ non sono virtuali (database partizionato) detto anche il middleware scenario, definito come segue

• si ha un set di sorgenti di dati
• la query coinvolge due o più di queste sorgenti
• il risultato si ottiene integrando in qualche modo i risultati parziali delle singole interrogazioni

per esempio la query

SELECT * FROM MyCars
WHERE Price < 15000
AND FuelConsumption < 7

Viene risolta per mezzo del seguente sistema

flowchart TD
A[(Mediator)]
B[wrapper]
C[wrapper]
D[(source 1)]
E[(source 2)]
A -- "select * from MyCars where Price < 15000"--> B
A --"select * from MyCars where FuelConsumption < 7"--> C
B --> D
C --> E

il caso del middleware scenario non e diverso dal caso delle top-$k$ join 1-1 query, con la differenza che nel caso delle query gli input sono locali, tuttavia le logiche algoritmiche sono le stesse :)

input di query top-$k$: assunzioni

• Si da per certo che le sorgenti dati (nel caso locale le relazioni) supportino un accesso ordinato per il parametro di ranking parziale $j$
• inoltre gli oggetti sono identificati in maniera globale fra le sorgenti dati per mezzo della OID
• tutte le sorgenti hanno lo stesso set di oggetti

Scoring functions

Alcune scelte comuni di scoring function sono:

• SUM(AVG)
• WSUM(Weighted sum)
• MIN(Minimum)
• MAX(Maximum)

Algoritmo $B_0$

in caso di funzione di scoring MAX la query e risolvibile per mezzo dell’algoritmo $B_0$, l’idea di base e quella di recuperare i primi $k$ migliori risultati parziali da ogni sorgente (ogni accesso e detto round) e computare il risultato senza effettuare accessi random

Input: ranked lists Lj (j=1,…,m), integer k  1
Output: the top-k objects according to the MAX scoring function
# B is a main-memory buffer
B = []
for j in range(1,m):
	
	# the set of objects "seen" on Lj
	Obj[j] = {}
	
	for i in range(1,k):
		# get the best k objects from each list
		t = getNextLj();
		Obj[j].append(t.OID)
		if t.OID not in B:
			# adds t to the buffer
			B.append(t)
		else: 
			# join t with the entry in B having the same OID;
# for each object with at least one partial score compute MAX using the available scores
for object in Obj:
	MAX(object) 
return #the k objects with maximum score

Numero minimo di round

E possibile fermare l’algoritmo prima di effettuare $k$ round a patto che sia verificata la seguente condizione

un algoritmo per top- $k$ 1-1 join queries che usa la funzione MAX come scoring function può essere stoppato se $Res[k].score\ge {\max }_j(p_j)$

Migliorando B0: MaxOptimal

Il teorema di cui sopra si può applicare seguendo un principio simile a quello visto per KNNOptimal dove ad ogni step si effettua un accesso ordinato sulla lista dove $p_j$ e massimo (la più promettente)

Perche B0 non funziona con altre scoring function

$B_0$ non funziona con funzioni diverse dalla funzione MAX perche al termine degli accessi sequenziali non vi e nessun limite inferiore al valore della scoring function, di conseguenza un oggetto che non e stato rilevato da un accesso sequenziale puo essere il match migliore

esempio con la funzione MIN

Algoritmo FA

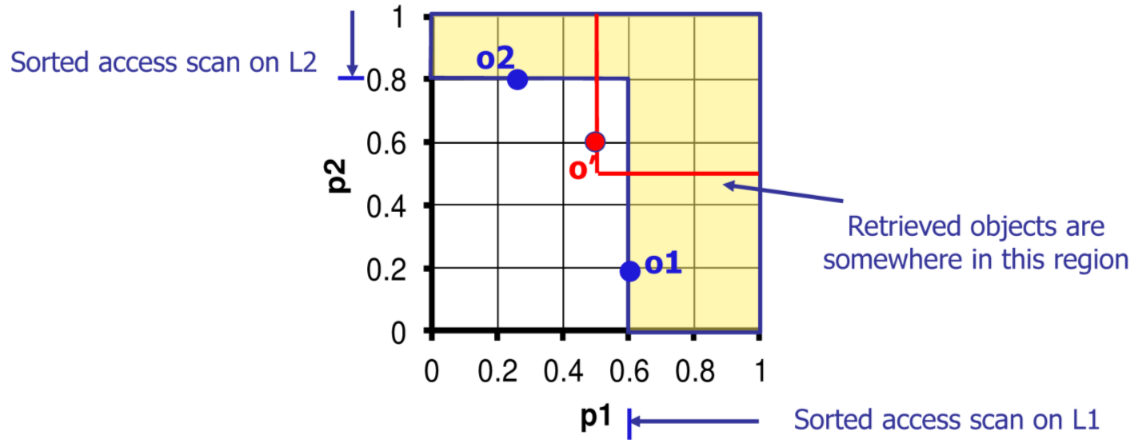
L’algoritmo FA sfrutta la proprietà di monotonicita della funzione di scoring per recuperare i best match, data la definizione di funzione di scoring monotona come segue

$$x_1\le y_1,x_2\le y_2,...,x_m\le y_m\Rightarrow S(x_1,x_2,...,x_m)\le S(y_1,y_2,...,y_m)$$

L’algoritmo recupera i primi $k$ score parziali dalle $m$ liste e per ogni oggetto con uno score parziale esegue un accesso random per recuperare gli altri, per ogni oggetto computa $S$ e restituisce i record con lo score massimo

Problematiche dell’algoritmo FA

L’algoritmo risulta computazionalmente esoso in quanto non viene sfruttata la funzione di scoring per ridurre lo spazio di ricerca, e non vengono anticipati i random access

Algoritmo TA

L’algoritmo TA e un miglioramento dell’Algoritmo FA, basato su threshold, in particolare

• esegue in maniera combinata accessi ordinati e random
• si ferma al raggiungimento di una threshold T che e un upper bound per gli oggetti non ancora visti

# Input: ranked lists Lj (j=1,…,m), integer k  1, monotone scoring function S
# Output: the top-k objects according to S
for i in range(1,k):
	Res[i] := [null,0]
	for j in range(1,m):
		pj := 1
		while Res[k].score < T := S(p1,p2,…,pm):
			for j in range(1,m):
				t := getNextLj()
				o := t.OID
# perform random accesses to retrieve the missing partial scores for o
				if S(o) := S(p1(o),…,pm(o)) > Res[k].score then:
					# {remove the object in Res[k]; insert [o,S(o)] in Res}
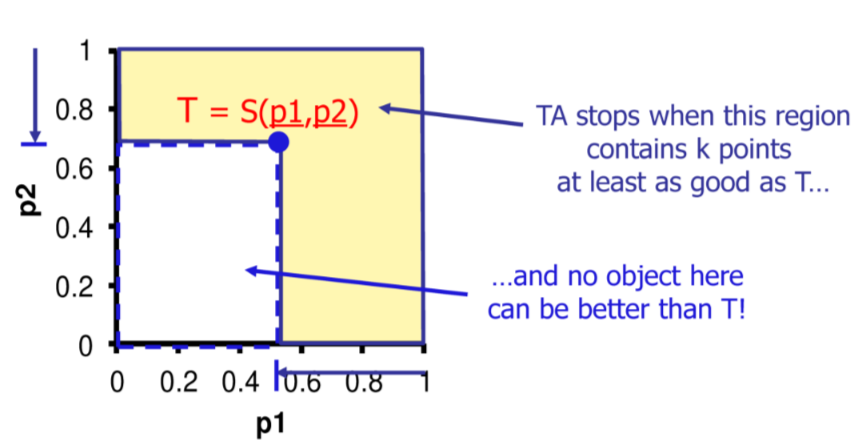
# return Res

L’algoritmo scandisce le liste fino a che la funzione di costo computata sui valori letti $S(p_1,p_2,...p_m)$ non e inferiore dello score dell’ultimo elemento del risultato (che e il peggiore risultato corretto)

Performance di TA

Per computare correttamente le performance di TA si considerano i costi di comunicazione con il client secondo la seguente funzione di costo:

$$cost=SA\ast C_{SA}+RA\ast C_{RA}$$

che considera costi di accessi sequenziali e randomici, i parametri $C_{SA},C_{RA}$ rappresentano il costo di singole letture sequenziali e ordinate, questi possono essere molto diversi a seconda degli scenari,

• in caso di risorse web tipicamente si ha che $C_{RA}>>C_{SA}$
• ma sono possibili risorse in cui non e possibile eseguire letture sequenziali $C_{SA}=\infty$

TA risulta essere instance optimal secondo la seguente definizione

data una classe di algoritmi $A$ e una classe $D$ di input un algoritmo $a\in A$ e instance optimal rispetto a $A$ e $D$ se e vero che per qualunque $B\in A$ e $DB\in D$ si ha $cost(a,DB)=O(cost(B,DB))$

dato il modello di costo di cui sopra nel caso in cui $C_{RA}>0$ ovvero il caso reale si ha che il costo di TA che si arresta al passo $X$ e:

$$cost(TA,DB)=m\ast X\ast C_{SA}+(m-1)X\ast m\ast C_{RA}$$

Assumendo il caso peggiore in cui per ogni oggetto visto sia necessario effettuare il massimo numero di accessi random, il ratio di ottimalita risulta essere

$$m+m(m-1)\frac{C_{RA}}{C_{SA}}$$

Che in caso di costi randomici alti puo diventare proibitivo

Algoritmo NRA

L’algoritmo NRA e pensato per quando non e possibile effettuare accessi randomici, restituisce comunque le $k$ risposte corrette ma i punteggi di score potrebbero essere errati

L’idea e quella di mantenere per ogni oggetto visto per mezzo della scansione sequenziale un lower e upper bound per la funzione di costo

• $S^{-}(O)$ computato ponendo a 0 (o al minimo valore possibile) tutti gli score parziali di $O$ non visti per mezzo della scansione sequenziale
• $S^{+}(O)$ computato ponendo $p_j(O)=p_j$ (il minimo dei valori visti per quella lista) tutti gli score parziali di $O$ non visti per mezzo della scansione sequenziale

Gli elementi trovati vengono mantenuti in una lista $B$ ordinati per valori di lowerbound

L’algoritmo termina quando le prime $k$ posizioni di $B$ contengono i valori migliori ovvero

$$S^{+}(o^{{}^{\prime }})\le S^{-}(o)\forall o^{{}^{\prime }}\notin Res,o\in Res$$

Ovvero tutti i valori visti non in res hanno un valore massimo di $S$ minore di quelli nel risultato

Ottenere le score corrette: NRA*

In caso siano necessari i valori di scoring e sufficiente estendere NRA eseguendo tante scansioni sequenziali fino a che tutti gli oggetti non vengono trovati

il costo e al piu uguale a Algoritmo FA

Algoritmo CA

L’idea dietro all’algoritmo CA e quella di ridurre il costo degli accessi randomici eseguendo le letture ogni $\frac{C_{RA}}{C_{SA}}$ rounds, per il resto l’algoritmo si comporta come NRA.

$B_0$, MaxOptimal, FA, TA, NRA, NRA*, CA al confronto

Algoritmo	scoring function applicabili	accesso ai dati	note
$B_0$	MAX	ordinato	instance optimal
MaxOptimal	MAX	ordinato	instance optimal
FA	monotone	ordinato e randomico	costo indipendente da $S$
TA	monotone	ordinato e randomico	instance optimal
NRA	monotone	ordinato	instance optimal,wrong scores
NRA*	monotone	ordinato	instance optimal, exact scores
CA	monotone	ordinato e randomico	instance optimal ratio di ottimalita indipendente da $\frac{C_{RA}}{C_{SA}}$ in alcuni casi

Ma in caso di join M-N?

Gli algoritmi visti fino ad ora sono applicabili se i join sono 1-1, nel caso seguente

SELECT *
FROM RESTAURANTS R, HOTELS H
WHERE R.City = H.City
AND R.Nation = 'Italy'
AND H.Nation = 'Italy'
ORDER BY R.Price + H.Price
STOP AFTER 2

i join non sono più sulle PK delle relazioni

Caso semplice: Indici !

Se si dispone di indici per ogni attributo di join l’algoritmo risulta simile a quello TA, sfruttando gli indici per gli accessi randomici

Caso difficile: non sono concessi accessi randomici

In questo caso e necessario adoperare solo per letture sequenziali (sulla linea di quanto visto per NRA*)

Rank-join

si computa una threshold $T$ definita come

$$\max (S(p_1,p_2^{max},...,,p_m^{max}),S(p_1^{max},p_2,...,,p_m^{max}),S(p_1^{max},p_2^{max},...,,p_m))$$

dove $p_j^{max}$ e definito come il primo valore visto in $L_j$

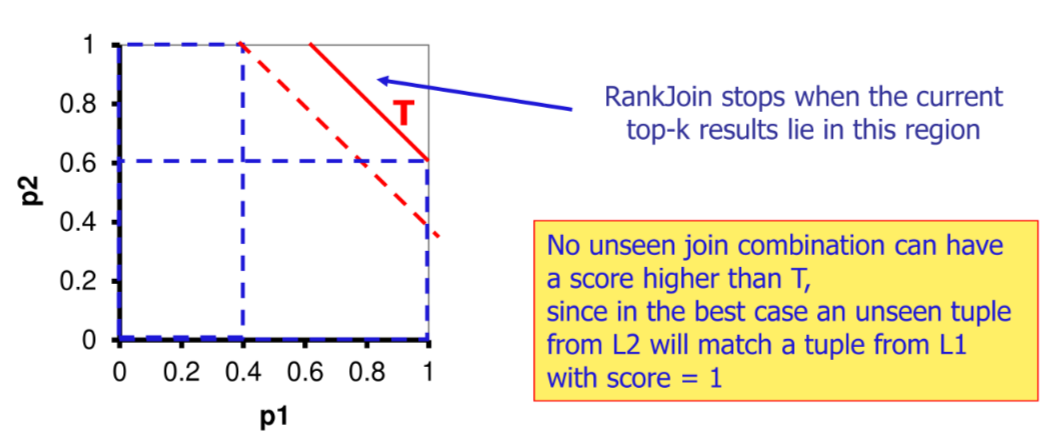
per far si che il rank join sia instance optimal e necessario che le relazioni siano al massimo 2 e che ci sia solo uno score parziale per input

PREVIOUS NEXT